TCML Announce New Channel. Splenius capitis Levator scapula Anterior middle and posterior scalenes.

Posterior Triangle Of The Neck Subdivisions Teachmeanatomy

You need to get 100 to score the 20 points available.

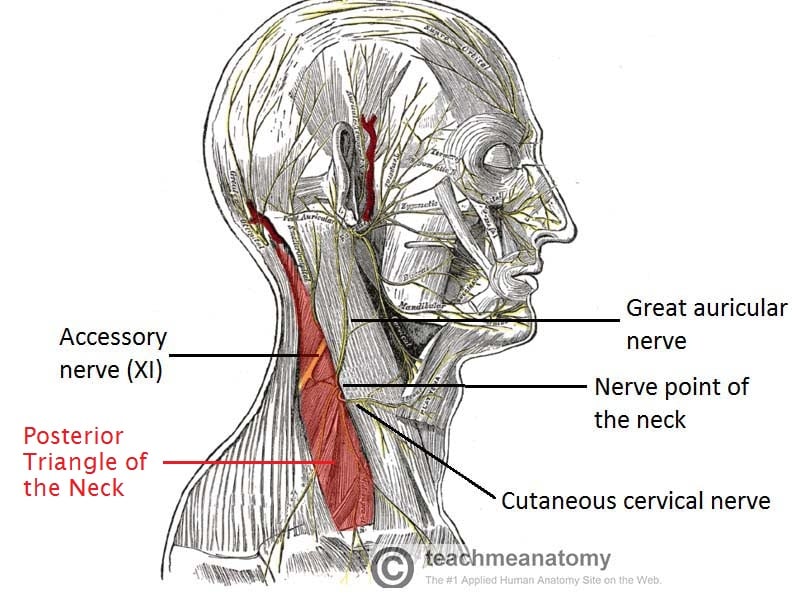
Posterior triangle of the neck. It is an anatomical area that is very clearly defined by three key anatomical landmarks. The nerve exits underneath the lateral border of the sternocleidomastoid muscle into. The inferior triangle is known as the subclavian triangle and contains the distal portion of the subclavian artery.

Its anterior boundary is formed by the sternocleidomastoid muscles. The triangles of the neck are the topographic areas of the neck bounded by the neck muscles. Posterior Triangle of the Neck Head and neck.

The posterior triangle is bounded at the back by the anterior border of the trapezius muscle. Iatrogenic Injuries of the Nerves. Your Skills Rank.

Its base downwards in the direction of the clavicle and apex is pointed upwards and backwards in the direction of the mastoid process. The landmarks that define the posterior triangle of the neck are as follows. Muscles of AnteriorPosterior Triangles of Neck learn by taking a quiz.

Online quiz to learn Muscles of AnteriorPosterior Triangles of Neck. The triangular space in front of this muscle is called the anterior triangle. The posterior triangle of the neck is home to parts of several muscles.

SC sternocleidomastoid muscle posterior border. Superior posterior belly of the digastric muscle. Therefore it could be injured in surgery requiring the removal or biopsy of lymph nodes in the posterior triangle of the neck.

Sn supraclavicular branch of the cervical plexus. Figure 4-37 The spinal accessory nerve crossing the posterior triangle of the neck on the right side. And at the base youve got the middle third of the clavicle.

Lateral medial border of the sternocleidomastoid muscle. The anterior triangle is subdivided by the hyoid bone suprahyoid and infrahyoid muscles into four triangles. The brachial plexus lies between the scalenus anterior and medius muscles.

The posterior triangle is crossed about 25 cm above the clavicle by the inferior belly of the omohyoid muscle which divides the space into two triangles. Splenius capitis levator scapulae middle and posterior scalene a small part of the serrates anterior Wry neck or torticollis affected the. Often multiple and associated with underlying infection or malignancy.

Note the supraclavicular branch of the cervical plexus following a similar but more superficial course. A solitary painless rubbery smooth mass. The larger superior part is termed the occipital triangle.

The s ternocleidomastoid muscle divides the neck into the two major neck triangles. And that behind it the posterior triangle. An upper or occipital triangle a lower or subclavian triangle or omoclavicular triangle.

The posterior triangle of the neck actually rests on the lateral aspect the side of the neck. The floor of the posterior triangle has several muscles. Sa spinal accessory nerve.

In the posterior triangle the spinal accessory nerve is adherent to the deep aspect of the fascial roof formed by prevertebral layer of deep cervical fascia of the triangle and is surrounded by lymph nodes. In this all the lymph nodes in the anterior and posterior triangles of the neck along with the associated. The omohyoid muscle splits the posterior triangle of the neck into two.

The carotid triangle of the neck has the following boundaries. This is a tutorial on the posterior triangle of the neck. The posterior triangle of the neck is comprised of several nerves including the spinal accessory nerve the branches of the cervical plexus the phrenic nerve and the roots and trunks of the brachial plexus.

The posterior triangle refers to the area of the neck posterior to the sternocleidomastoid muscle. Behind the sternocleidomastoid muscle the triangular space on the side of neck is called the Posterior triangle. Anteriorly its bounded by the posterior margin of the sternocleidomastoid muscle so this muscle here.

The anterior triangle and the posterior triangle of the neck each of them containing a few subdivisions.

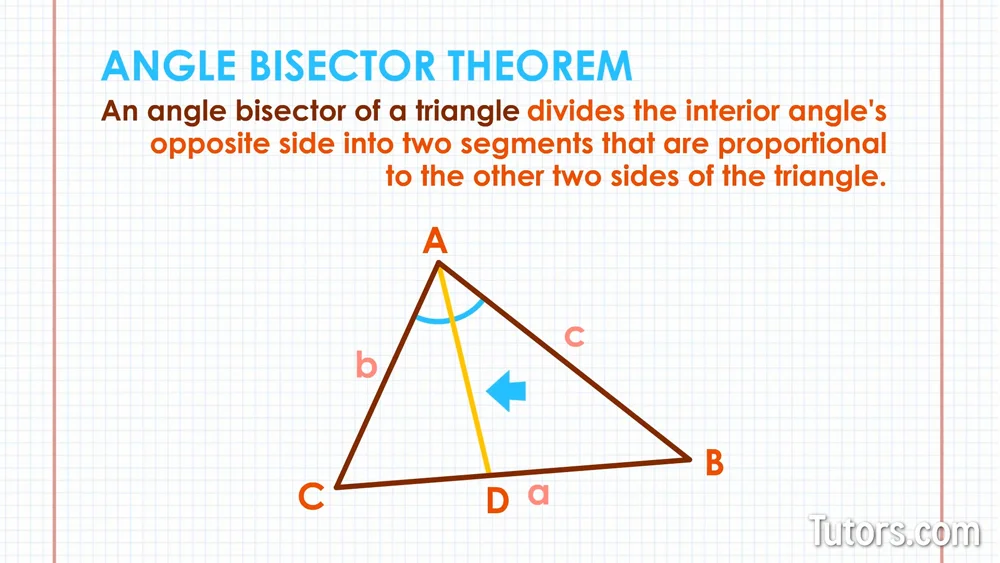
An angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle. In other words mACE mBCE.

Angle Bisector Theorem Definition Examples Video Tutors Com

EAD CAD AD bisector.

Angle bisector of a triangle. Calculate the length of bisector if given hypotenuse and angle at the hypotenuse L. The angle bisector theorem is concerned with the relative lengths of the two segments that a triangles side is divided into by a line that bisects the opposite angle. The angle bisector of a triangle can be constructed as follows.

The following figure illustrates this. Let it be angle A. An angle bisector in a triangle divides the opposite side into two parts whose lengths are in the same ratio as the lengths of the two sides that form the angle.

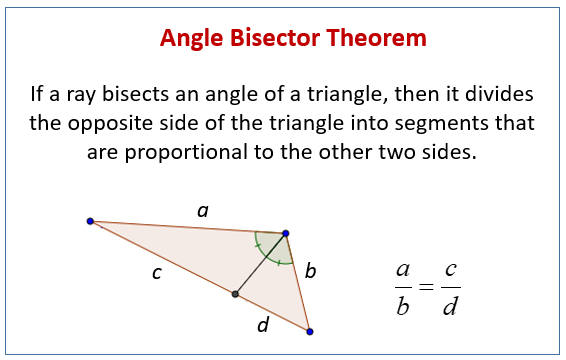
The angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment CD is equal to the ratio of the length of side AB to the length of side AC. The point of concurrency of the angle bisectors is called the incenter of the triangle and it always lies inside the triangle. The angle bisector theorem state that in a triangle the angle bisector partitions the opposite side of the triangle into two segments with a ratio that is the same as the ratio between the two sides forming the angle it bisects.

It follows from the equality of the triangles. This Euclidean construction works by creating two congruent triangles. AD common side.

Angle bisector A D cuts side a into two line segments C D and D B. Construction Steps of. The three angle bisectors are concurrent.

In a triangle an angle bisector is a line which bisects an angle of the triangle. The Angle-Bisector theorem states that if a ray bisects an angle of a triangle then it divides the opposite side into segments that are proportional to the other two sides. Extend C A to meet B E at point E.

It has been illustrated in the diagram shown below. Central Projection Matrix construction. An angle bisector of a triangle is a segment that bisects an angle of that triangle and extends to the opposite side.

A C D and A B D created by the angle bisector are also similarly proportional. It equates their relative lengths to the relative lengths of the other two sides of the triangle. And conversely if a point D on the side BC of triangle ABC divides BC in the same ratio as the sides AB and AC then AD is the angle bisector of angle A.

Step 1 Select an angle in the triangle in which the angle bisector should be constructed. The Angle-Bisector theorem involves a proportion like with similar triangles. It explains in simple ways to draw the bisector of angles of a triangle.

So 4 1. An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle. To bisect an angle means that we divide the angle into two equal congruent parts without actually measuring the angle.

This video is related to geometry chapter. In your problem AD is the angle bisector. Learn about loci three figure bearings and revise drawing line segment angle bisector and perpendicular point constructions with BBC Bitesize KS3 Maths.

Auxiliary lines will be needed to create similar triangles. Draw B E A D. Converting Decimals to Fractions.

AE AC by condition. See the proof below for more on this. In triangle ABC angle B is 23 degrees angle C is 41 degrees AD is the bisector E is a point on AB such that AE AC.

C D and D B relate to sides b C A and c B A in the same proportion as C A and B A relate to each other. Segment CE bisects angle ACB and creates angle ACE and angle BCE that are congruent. We conclude that the triangles are equal.

With AB 50 AC 60 and BC 70 the angle bisector AD divides BC with length 70 into two pieces whose lengths are in the ratio 5060 or 56. In triangle ABC shown above segment CE is an angle bisector for that triangle. The angles 4 and 1 are corresponding angles.

The angle bisector is a line that divides an angle into two equal halves each with the same angle measure. An angle bisector of a triangle divides the interior angles opposite side into two segments that are proportional to the other two sides of the triangle. The bisector of a right triangle from the vertex of the acute angle if you know sides and angles.

Consider triangles AED and ACD in them.

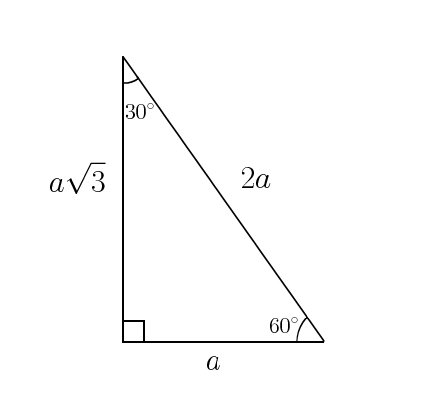
Once we identify a triangle to be a 30 60 90 triangle the values of all angles and sides can be quickly identified. Looking at the diagram we can see that we have a right-angled triangle in which the other two angles are 30 degrees and 60 degrees.

In A 30 60 90 Triangle Where The Shortest Leg Equals 3 What Could The Other Sides Equal Socratic

Find the length of the side x.

Side lengths of a 30-60-90 triangle. A special right triangle is a right triangle having angles of 30 60 90 or 45 45 90. Find the values of 𝑎 and 𝑏. The key characteristic of a 30-60-90 right triangle is that its angles have measures of 30 degrees π6 rads 60 degrees π3 rads and 90 degrees π2 rads.

The following diagram shows a 30-60-90 triangle and the ratio of the sides. The 30-60-90 degree triangle is in the shape of half an equilateral triangle cut straight down the middle along its altitude. The 45-45-90 triangle also referred to as an isosceles right triangle since it has two sides of equal lengths is a right triangle in which the sides corresponding to the angles 45-45-90 follow a ratio of 11 2.

If the longer leg length b is the one parameter given then. It is special because its side lengths are always in the ratio of 1. Each half has now become a 30 60 90 triangle.

It is right triangle whose angles are 30 60 and 90. A 30-60-90 triangle is a particular right triangle because it has length values consistent and in primary ratio. To understand the 30-60 ideal triangle we need to assess a previous topic the equilateral or equiangular triangular.

This doesnt need to be precise however the closer the far better. If we know the shorter leg length a we can find out that. A 30-60-90 right triangle literally pronounced thirty sixty ninety is a special type of right triangle where the three angles measure 30 degrees 60 degrees and 90 degrees.

A 30-60-90 triangle is a special triangle whose angles are 30º 60º and 90º. Because its angles and side ratios are consistent test makers love to incorporate this triangle into problems especially on the no-calculator portion of the SAT. A 30-60-90 triangle is a special right triangle that contains internal angles of 30 60 and 90 degrees.

Lets start by attracting a triangle with all three sides the same length. Imagine cutting an equilateral triangle vertically right down the middle. The side lengths and angle measurements of a 30-60-90 right triangle.

30 60 90 triangle sides. Like the 30-60-90 triangle knowing one side length allows you to determine the lengths of the other sides. Or simply type your given values and the 30 60 90 triangle calculator will do the rest.

The side lengths of a 306090 triangle This is a triangle whose three angles are in the ratio 1. We can see therefore that the side lengths for a 30-60-90 triangle will always have consistent side lengths of x x3 and 2x or x2 3x2 and x. The shortest leg is across from the 30-degree angle the length of the hypotenuse is always double the.

For hypotenuse c known the legs formulas look as follows. Since the triangle is equilateral it is also equiangular and therefore the the angle at B is 60 The height of a triangle is the straight line drawn from the vertex at right angles to the base. 3 and respectively measure 30 π 6 60 π 3 and 90 π 2.

Scroll down the page for more examples and solutions on how to use the 30-60-90 triangle. Luckily for us we can prove 30-60-90 triangle rules true without all ofthis. The leg opposite the 60 angle is of the length of the hypotenuse.

In any 30-60-90 triangle the shortest leg is still across the 30-degree angle the longer leg is the length of the short leg multiplied to the square root of 3 and the hypotenuses size is always double the length of the shorter leg. The sides are in the ratio 1. The ratio of the side lengths of a 30-60-90 triangle are.

Knowledge of the ratio o. In any 30-60-90 triangle you see the following. The Side Lengths of 30-60-90 Triangles Mathematics Find the values of 𝑎 and 𝑏.

The hypotenuse is twice the length of the shortest side. The hypotenuse of the triangle that is the longest side. The lengths of the sides of a 30-60-90 triangle are in the ratio of 132.

The 30-60-90 triangle is a special right triangle and knowing it can save you a lot of time on standardized tests like the SAT and ACT. It has angles of 30 60 and 90. Therefore triangle ADB is a 30-60-90 triangle.

When to Use 30-60-90 Triangle Rules. The theory applies to the side lengths of a 30 60 90 triangle. The leg opposite the 30 angle the shortest side is the length of the hypotenuse the side opposite the 90 angle.

Learn about the special right triangles. The sides of a 30-60-90 right triangle lie in the ratio 132. The triangle is significant because the sides exist in an easy-to-remember ratio.

Luckily for us we can prove 30-60-90 triangle rules true without all ofthis. We can see therefore that a 30-60-90 triangle will always have consistent side lengths of x x3 and 2x or x2 3x2 and x. The ratios of the sides can be calculated using two congruent 30-60-90 triangles.