If every internal angle of a simple polygon is less than 180 the polygon is called convex. The formula for calculating the size of an exterior angle is.
 Find The Measure Of Each Exterior Angle Of The Given Regular Polygon Level 1 Youtube
Find The Measure Of Each Exterior Angle Of The Given Regular Polygon Level 1 Youtube
Exterior angle of regular polygon is given by frac 360 0 n where n is number of sides of a regular polygon.

What is the exterior angle of a regular polygon. The sum of the exterior angles of a regular polygon irrespective of the number of sides is 360 degrees. A Polygon is any flat shape with straight sides. The Exterior Angles of a Polygon add up to 360.
Interior Angles of a Regular Polygon. As you can see for regular polygons all the exterior angles are the same and like all polygons they add to 360 see note below. Regular polygons may be either convex or starIn the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon effectively a straight line.
All the Exterior Angles of a polygon add up to 360 so. The sum of the measures of the interior angles of a polygon with n sides is n 2180. Exterior Angles of a Regular Polygon Exterior angles of every simple polygon add up to 360 360 because a trip around the polygon completes a rotation or return to your starting place.
Where sides meet they form vertices so our hexagon also has six vertices. Each exterior angle must be 360n where n is the number of sides Press play button to see. In Euclidean geometry a regular polygon is a polygon that is equiangular all angles are equal in measure and equilateral all sides have the same length.
The sum of the exterior angles of a polygon is 360. By using this formula easily we can find the exterior angle of regular polygon. For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45.
As a demonstration of this drag any vertex towards the center of the polygon. So each exterior angle is 360 divided by the n the number of sides. The sum of the measures of the exterior angles of a polygon one at each vertex is 360.
Exterior angle of a polygon 360 number of sides. In contrast an exterior angle also called an external angle or turning angle is an angle formed by one side of a simple polygon and a line extended from an adjacent side. They are Supplementary Angles.
An exterior angle is an angle formed between any side and the line extended to its adjacent side. For any given regular polygon to find the each exterior angle we have a formula. On a side note we can use this piece of information in the exterior angle of a polygon formula to solve various questions.
You will see that the angles combine to a full 360 circle. Measure of exterior angle of regular polygon is calculated by dividing the sum of the exterior angles by the number of sides and is represented as MOE360n or Measure of exterior angle 360Number of sides. Since it is a regular polygon the number of sides can be calculated by the sum of all exterior angles which is 360 degrees divided by the measure of each exterior angle.
In the present case there 5 sides in a regular pentagon hence each exterior 3605 or 72 degrees. When the polygons are formed and one of its sides is extended longer than the vertex of a corner the exterior angle of the polygon is formed. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has.
A polygon has exactly one internal angle per vertex. An exterior angle of a polygon is an angle outside the polygon formed by one of its sides and the extension of an adjacent side. There are as many exterior angles as there are sides n and they are all equal.
If N is the number of sides each exterior angle will be 360N degrees. The sum is divided by n to find each exterior angle. The result of the sum of the exterior angles of a polygon is 360 degrees.
Find the regular polygon where each of the exterior angle is equivalent to 60 degrees. In regular polygons the sum of the exterior angles equals 360º ie it forms a circle outside. Formula for exterior angle of regular polygon as follows.
When we add up the Interior Angle and Exterior Angle we get a straight line 180. The exterior angle at a vertex can be obtained by the following formula. The sum of the exterior angles of a regular polygon will always equal 360 degrees.
The sum of exterior angles of a polygon is 360. Measure of a Single Exterior Angle Formula to find 1 angle of a regular convex polygon of n sides 1 2 3 360. Exterior Angles of Polygons The Exterior Angle is the angle between any side of a shape and a line extended from the next side.
Exterior Angle 360 n Exterior Angle 360 n. The number of Sides is used to classify the polygons.
An angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle. In other words mACE mBCE.
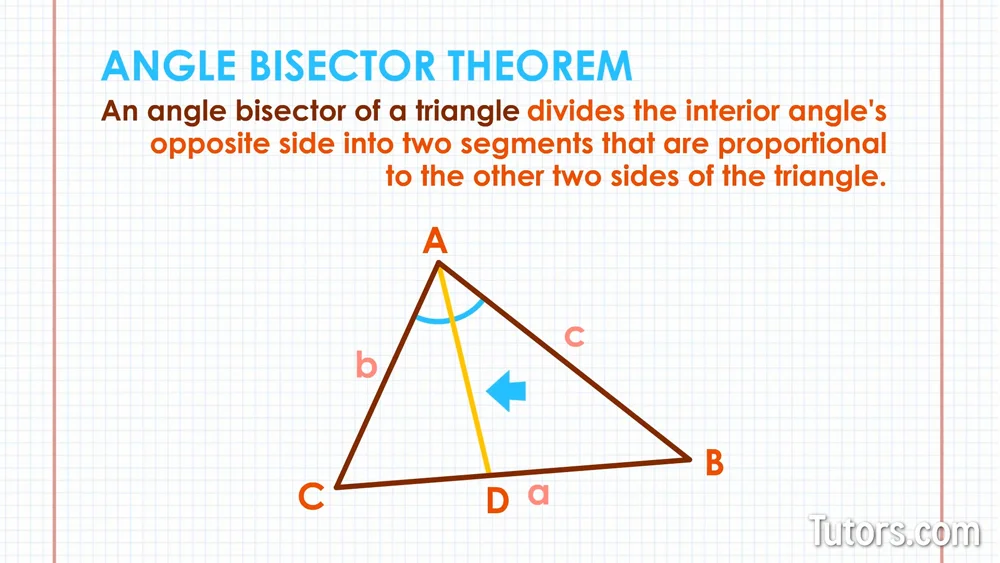 Angle Bisector Theorem Definition Examples Video Tutors Com
Angle Bisector Theorem Definition Examples Video Tutors Com
EAD CAD AD bisector.
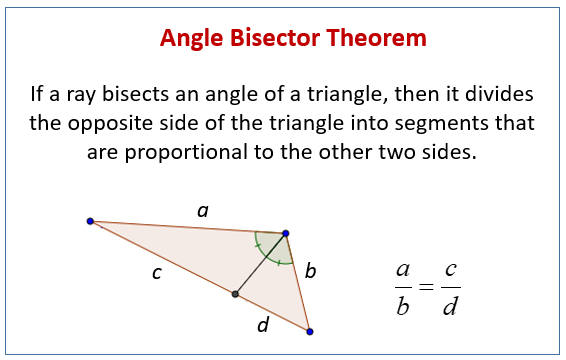
Angle bisector of a triangle. Calculate the length of bisector if given hypotenuse and angle at the hypotenuse L. The angle bisector theorem is concerned with the relative lengths of the two segments that a triangles side is divided into by a line that bisects the opposite angle. The angle bisector of a triangle can be constructed as follows.
The following figure illustrates this. Let it be angle A. An angle bisector in a triangle divides the opposite side into two parts whose lengths are in the same ratio as the lengths of the two sides that form the angle.
The angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment CD is equal to the ratio of the length of side AB to the length of side AC. The point of concurrency of the angle bisectors is called the incenter of the triangle and it always lies inside the triangle. The angle bisector theorem state that in a triangle the angle bisector partitions the opposite side of the triangle into two segments with a ratio that is the same as the ratio between the two sides forming the angle it bisects.
It follows from the equality of the triangles. This Euclidean construction works by creating two congruent triangles. AD common side.
Angle bisector A D cuts side a into two line segments C D and D B. Construction Steps of. The three angle bisectors are concurrent.
In a triangle an angle bisector is a line which bisects an angle of the triangle. The Angle-Bisector theorem states that if a ray bisects an angle of a triangle then it divides the opposite side into segments that are proportional to the other two sides. Extend C A to meet B E at point E.
It has been illustrated in the diagram shown below. Central Projection Matrix construction. An angle bisector of a triangle is a segment that bisects an angle of that triangle and extends to the opposite side.
A C D and A B D created by the angle bisector are also similarly proportional. It equates their relative lengths to the relative lengths of the other two sides of the triangle. And conversely if a point D on the side BC of triangle ABC divides BC in the same ratio as the sides AB and AC then AD is the angle bisector of angle A.
Step 1 Select an angle in the triangle in which the angle bisector should be constructed. The Angle-Bisector theorem involves a proportion like with similar triangles. It explains in simple ways to draw the bisector of angles of a triangle.
So 4 1. An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle. To bisect an angle means that we divide the angle into two equal congruent parts without actually measuring the angle.
This video is related to geometry chapter. In your problem AD is the angle bisector. Learn about loci three figure bearings and revise drawing line segment angle bisector and perpendicular point constructions with BBC Bitesize KS3 Maths.
Auxiliary lines will be needed to create similar triangles. Draw B E A D. Converting Decimals to Fractions.
AE AC by condition. See the proof below for more on this. In triangle ABC angle B is 23 degrees angle C is 41 degrees AD is the bisector E is a point on AB such that AE AC.
C D and D B relate to sides b C A and c B A in the same proportion as C A and B A relate to each other. Segment CE bisects angle ACB and creates angle ACE and angle BCE that are congruent. We conclude that the triangles are equal.
With AB 50 AC 60 and BC 70 the angle bisector AD divides BC with length 70 into two pieces whose lengths are in the ratio 5060 or 56. In triangle ABC shown above segment CE is an angle bisector for that triangle. The angles 4 and 1 are corresponding angles.
The angle bisector is a line that divides an angle into two equal halves each with the same angle measure. An angle bisector of a triangle divides the interior angles opposite side into two segments that are proportional to the other two sides of the triangle. The bisector of a right triangle from the vertex of the acute angle if you know sides and angles.
Consider triangles AED and ACD in them.
We can then rotate that side through an angle of B to reach the next side. S n 2 180 This is the angle sum of interior angles of a polygon.
Conjectures In Geometry Exterior Angles
In any polygon the sum of exterior angles is.
Exterior angle of polygon formula. In a 20-sided polygon one vertex does not send any diagonals. Exterior angle of a polygon 360 number of sides. The exterior angle of the regular polygon with 24 sides is given as the frac 360 0 24 15 0.
How to solve the exterior angles of a polygon. According to the formula number of diagonals n n-3 2. The sum of the internal angle and the external angle on the same vertex is 180.
Sum of Interior angles of Polygon IA n-2 x 180 The measure of an exterior angle of a regular n - sided polygon is given by the formula 360n Exterior angle of a regular polygon EA 360n. The measure of each exterior angle is 72. For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45.
Exterior Angles Sum of Polygons. The sum of the exterior angles of a regular polygon will always equal 360 degrees. An exterior angle of a polygon is made by extending only one of its sides in the outward direction.
The sum of the measures of the interior angles of a polygon with n sides is given by the general formula n2180. For an n-gon the sum of the measures of the exterior angles is sum 360. So 11-sided polygon will contain 1111-32 44 diagonals.
The sum of exterior angles of a polygon is 360. The sum of all the internal angles of a simple polygon is 180n2 where n is the number of sidesThe formula can be proved using mathematical induction and starting with a triangle for which the angle sum is 180 then replacing one side with two sides connected at a vertex and so on. The sum of the measures of the exterior angles of a polygon one at each vertex is 360.
Measure of a Single Exterior Angle Formula to find 1 angle of a regular convex polygon of n sides 1 2 3 360. Measure of exterior angle of regular polygon is calculated by dividing the sum of the exterior angles by the number of sides and is represented as MOE360n or Measure of exterior angle 360Number of sides. Hence we can say now if a convex polygon has n sides then the sum of its interior angle is given by the following formula.
360 5. The sum of the measures of the interior angles of a polygon with n sides is n 2180. Formula 3 examples and their solutions.
Notice that corresponding interior and exterior angles are supplementary add to 180. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has. The exterior angle of the regular polygon with 16 sides is given as the frac 360 0 16 225 0.
Find out how many diagonals does that 20-sided polygon contain. The measure of each exterior angle of a regular pentagon is 2x 4. Interior and exterior angle formulas.
The formula for calculating the size of an exterior angle is. Yes we can say what type of polygon. The formula for calculating the size of an exterior angle of a regular polygon is.
Formula 3 examples and their solutions. Formula to find the measure of each exterior angle of a regular n-sided polygon is. For an n-gon the sum of the measures of the exterior angles is sum 360.
If we know exterior angle then can we say what type of polygon is it. Starting at the top side red we can rotate clockwise through an angle of A to reach the angle of the adjacent side to the right. Each exterior angle must be 360n where n is the number of sides Press play button to see.
FAQs on Exterior angle of regular polygon. Lets take a regular hexagon for example. The number of Sides is used to classify the polygons.
So total diagonals contained within an 11-sided polygon 55 -11 ie. Exterior Angle Sum Property of Polygon - formula Exterior angle of polygon n 3 6 0 o. An exterior angle of a polygon is an angle outside the polygon formed by one of its sides and the extension of an adjacent side.
All the Exterior Angles of a polygon add up to 360 so. Solution Detail These four angles are the interior angles of the quadrilateral. Exteriorangleofaregularpolygon 360div numberofsides Remember the interior and exterior.
How to solve the exterior angles of a polygon. An exterior angle of a polygon is an angle at a vertex of the polygon outside the polygon formed by one side and the extension of an adjacent side.