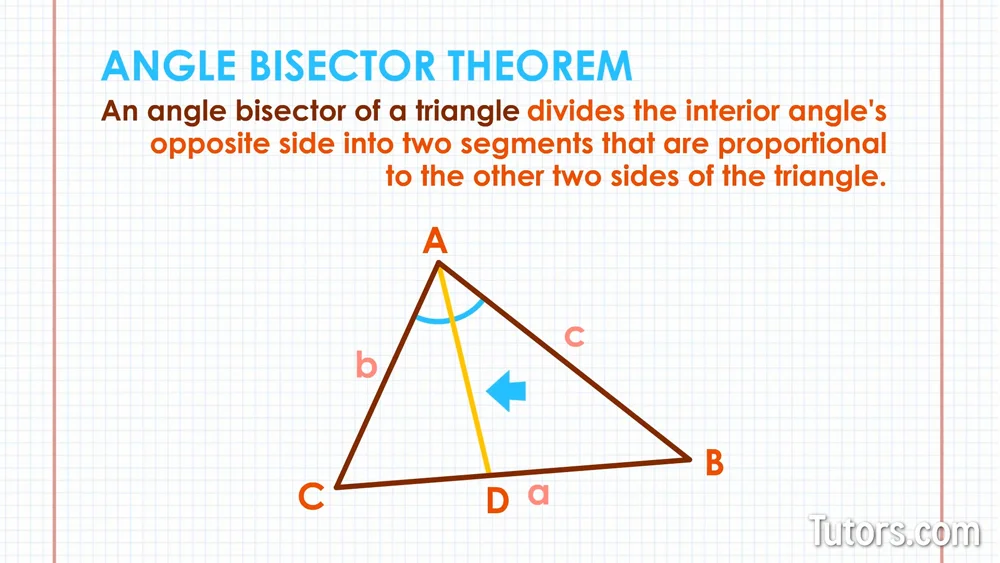
An angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides of the triangle. In other words mACE mBCE.

Angle Bisector Theorem Definition Examples Video Tutors Com

EAD CAD AD bisector.

Angle bisector of a triangle. Calculate the length of bisector if given hypotenuse and angle at the hypotenuse L. The angle bisector theorem is concerned with the relative lengths of the two segments that a triangles side is divided into by a line that bisects the opposite angle. The angle bisector of a triangle can be constructed as follows.

The following figure illustrates this. Let it be angle A. An angle bisector in a triangle divides the opposite side into two parts whose lengths are in the same ratio as the lengths of the two sides that form the angle.

The angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment CD is equal to the ratio of the length of side AB to the length of side AC. The point of concurrency of the angle bisectors is called the incenter of the triangle and it always lies inside the triangle. The angle bisector theorem state that in a triangle the angle bisector partitions the opposite side of the triangle into two segments with a ratio that is the same as the ratio between the two sides forming the angle it bisects.

It follows from the equality of the triangles. This Euclidean construction works by creating two congruent triangles. AD common side.

Angle bisector A D cuts side a into two line segments C D and D B. Construction Steps of. The three angle bisectors are concurrent.

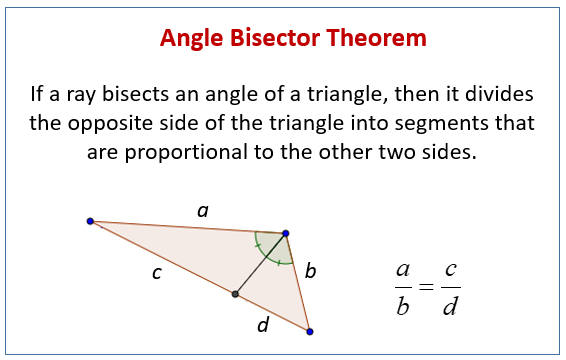
In a triangle an angle bisector is a line which bisects an angle of the triangle. The Angle-Bisector theorem states that if a ray bisects an angle of a triangle then it divides the opposite side into segments that are proportional to the other two sides. Extend C A to meet B E at point E.

It has been illustrated in the diagram shown below. Central Projection Matrix construction. An angle bisector of a triangle is a segment that bisects an angle of that triangle and extends to the opposite side.

A C D and A B D created by the angle bisector are also similarly proportional. It equates their relative lengths to the relative lengths of the other two sides of the triangle. And conversely if a point D on the side BC of triangle ABC divides BC in the same ratio as the sides AB and AC then AD is the angle bisector of angle A.

Step 1 Select an angle in the triangle in which the angle bisector should be constructed. The Angle-Bisector theorem involves a proportion like with similar triangles. It explains in simple ways to draw the bisector of angles of a triangle.

So 4 1. An angle bisector of an angle of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle. To bisect an angle means that we divide the angle into two equal congruent parts without actually measuring the angle.

This video is related to geometry chapter. In your problem AD is the angle bisector. Learn about loci three figure bearings and revise drawing line segment angle bisector and perpendicular point constructions with BBC Bitesize KS3 Maths.

Auxiliary lines will be needed to create similar triangles. Draw B E A D. Converting Decimals to Fractions.

AE AC by condition. See the proof below for more on this. In triangle ABC angle B is 23 degrees angle C is 41 degrees AD is the bisector E is a point on AB such that AE AC.

C D and D B relate to sides b C A and c B A in the same proportion as C A and B A relate to each other. Segment CE bisects angle ACB and creates angle ACE and angle BCE that are congruent. We conclude that the triangles are equal.

With AB 50 AC 60 and BC 70 the angle bisector AD divides BC with length 70 into two pieces whose lengths are in the ratio 5060 or 56. In triangle ABC shown above segment CE is an angle bisector for that triangle. The angles 4 and 1 are corresponding angles.

The angle bisector is a line that divides an angle into two equal halves each with the same angle measure. An angle bisector of a triangle divides the interior angles opposite side into two segments that are proportional to the other two sides of the triangle. The bisector of a right triangle from the vertex of the acute angle if you know sides and angles.

Consider triangles AED and ACD in them.