Properties Property 1 The angles on the same side of a leg are called adjacent angles and are supplementary more Property 2 Area of a Trapezoid A r e a h e i g h t sum bases 2 more Property 3 Trapezoids have a midsegment which connects the mipoints of the legs more. The sides and angles of a trapezoid.
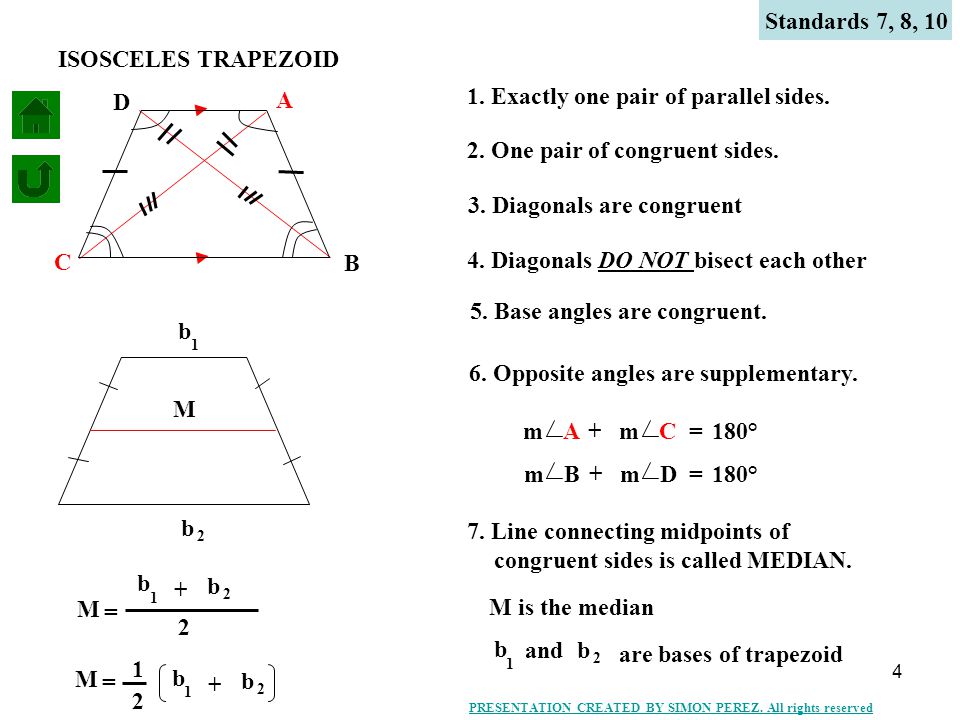
Each lower base angle is supplementary to the upper base angle on the same side.
Properties of a regular trapezoid. The links will open a new browser window. It has two pairs of sides. Properties of a Trapezoid The formula for the perimeter of a trapezoid is P a b c d.
If the legs are congruent we have what is called an isosceles trapezoid. A parallelogram may also be called a trapezoid as it has two parallel sides. Base angles of a trapezoid are congruent.
The properties of parallelograms can be applied on rhombi. It has four right angles 90. Figure is an isosceles trapezoid.
Properties of Regular Polygons Polygon. A trapezoid is a four-sided shape quadrilateral such that one pair of opposite sides are parallel. A related notion is the one of a minimum bounding circle which is the smallest circle that completely contains the polygon within it if the circles center is within the polygon.
No sides need to be congruent and no angles need to be congruent. The diagonals shown as dashed lines above meet at a right angle. The bases of a trapezoid are parallel.
One of the diagonals bisects cuts equally in half the other. The base angles have the same measure. The angles where the two pairs meet are equal.
Properties of Trapezoids Recall that a trapezoid is a quadrilateral with only one pair of opposite sides parallel and that the parallel sides are called bases and the nonparallel sides are called legs. A polygon is a plane shape two-dimensional with straight sides. The lengths of opposite sides are equal.
The perimeter of a rectangle is the sum of twice the length and twice the width. The diagonals of an isosceles trapezoid are congruent. A square has four sides of equal length.
The bases top and bottom of a trapezoid are parallel. The Properties of Trapezoids and Isosceles Trapezoids The properties of the trapezoid are as follows. Each lower base angle is.
All triangles all regular simple polygons all rectangles all isosceles trapezoids and all right kites are cyclic. If we have a quadrilateral where one pair and only one pair of sides are parallel then we have what is called a trapezoid. To find the perimeter of a trapezoid just add the lengths of all four sides together.
Each calculator is associated with web pageor on-page equations for calculating the sectional properties. Trapezium and Its Properties A trapezium or a trapezoid is a quadrilateral with a pair of parallel sides. The following links are to calculators which will calculate the Section Area Moment of Inertia Properties of common shapes.
Any one of the following properties distinguishes an isosceles trapezoid from other trapezoids. If the legs of a trapezoid are equal it is called an isosceles trapezoid. Depending on how the trapezium is drawn determines how many lines of symmetry if has.
An acute trapezoid has two adjacent acute angles on its longer base edge while an obtuse trapezoid has one acute and one obtuse angle on each base. Shape with four sides. An isosceles trapezoid is a trapezoid where the base angles have the same measure.
A right trapezoid alsright-angled trapezoid has two adjacent right angles. And thats it for the special quadrilaterals. The diagonals of a trapezoid are perpendicular.
The segment that joins the midpoints of the parallel sides is perpendicular to them. The parallel sides are called bases while the nonparallel sides are called legs. Right trapezoids are used in the trapezoidal rule for estimating areas under a curve.
ALL isosceles trapezoids are regular trapezoids BUT isosceles trapezoids have their non-parallel sides equal in length in addition to having precisely one pair of opposite sides parallel. Learn how to solve problems with trapezoids. There are six special quadrilaterals with different properties.
The adjacent sides of a trapezoid are congruent. Nothing special happens with the diagonals. The main property of a trapezium as known in Great Britain or trapezoid as known in the United States is that it is a 4 side shape with exactly one pair of parallel sides.
Opposite angles are supplementary which in. The bases are parallel by definition. The pair of parallel sides is called the base while the non-parallel sides are called the legs of the trapezoid.
The diagonals have the same length. Properties of Rectangles Rectangles have four sides and four right angles. The bases are parallel by definition.
Each pair is made of two equal-length sides that join up. Examples include triangles quadrilaterals pentagons hexagons and so on.
If you know the length of one of the sides the area is given by the formula. 4 Plug the values of a and p in the formula and get the area.
In Euclidean geometry a regular polygon is a polygon that is equiangular all angles are equal in measure and equilateral all sides have the same length.
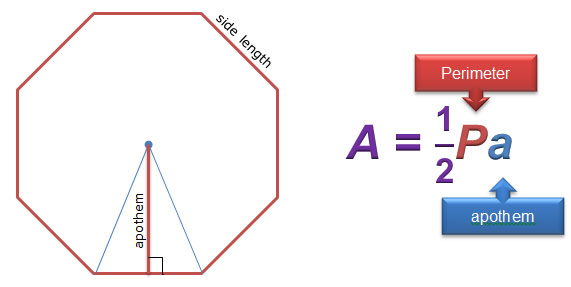
What is the area of a regular polygon. The following formula for equilateral triangles however uses only the side length. Area a x p2 where a is the length of the apothem and p is the perimeter of the polygon. In my next note I will prove that the area of any regular polygon can be represented as.
If the circum-radius r of the regular polygon is given then. Regular polygons use line segments that form sides enclosing a space the polygons interior. Area 12 x perimeter x apothem.
Find the area of a regular polygon with perimeter of 44 cm and apothem length of 10 cm. ½ x 44 x 10 cm 2. Apothem is a segment that joins the polygons center to the midpoint of any side and it is perpendicular to that side.
By definition all sides of a regular polygon are equal in length. A r 2 n sin360n2 Square units. 220 cm 2.
Area of Regular Polygon. Equivalently it is both cyclic and equilateral or both equilateral and equiangular. Use this calculator to calculate properties of a regular polygon.
2 3 6. Calculates side length inradius apothem circumradius area and perimeter. The Area of a regular polygon A S 2 n4tan180n Square units.
Equilateral and equal angles ie. An apothem is also used sometimes to find the area of a regular polygon. As we know Area A ½ x p x a here p 44 cm and a 10 cm.
The area of any regular polygon is given by the formula. Area of Polygon ½ n Radius 2 sin2 π n. Calculate the area of the regular polygon given that the number of sides is 5 and the side length is 3cm Solution.
The area of a regular 6-star polygon is 51960 sq. Equiangular is known as a regular polygon. Note that units of length are shown for.
Area of Polygon n Apothem 2 tanπn When we dont know the Apothem we can use the same formula but re-worked for Radius or for Side. The apothem is a line segment that joins the polygons center to the midpoint of any side that is perpendicular to that side. Perimeter the sum of the lengths of all the sides.
A 12. The area of a regular polygon formula is given as follows. Thank you for the challenge JubayerNirjhor.
Area of Regular Polygon Example. The apothem is 24142 centimeters. Enter any 1 variable plus the number of sides or the polygon name.
Area of a Regular Polygon Now the formula for finding the area of any regular polygon is half the product of the perimeter and apothem. Area of a regular polygon n s a 2 n s a 2. Regular polygons may be either convex or starIn the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon effectively a straight line.
Area of a polygon using the concept of the apothem. Where n n is the number of sides s s is the length of one side and a a is known as apothem it is the line from the center of the regular polygon that is perpendicular to one of its sides. Here is what it means.
Area is always expressed in square units such as cm2 f t2 in2 c m 2 f t 2 i n 2. The area of a regular polygon can be calculated using the concept of apothem. Area ½ apothem perimeter Several other area formulas are also available.
The area of regular hexagon if its side is 4 c m View solution Find the area of a regular polygon of 7 sides whose each side measures 4 c m and the circumradius is 3 c m 5 2. Calculate from an regular 3-gon up to a regular 1000-gon. As an example lets use a hexagon 6 sides with a side s length of 10.
Finding the area of regular polygon when the SIDE and APOTHEM are known. Area of a Regular Polygon The area of any closed shape is the interior space formed by the shapes sides. Where s is the length of any side.
Area of a Regular Polygon The area of a regular polygon is given by the formula below. Here is a list of the sections within this webpage. AREA OF REGULAR POLYGON Area of an Equilateral Triangle The area of any triangle with base length b and height h is given by A 12 bh.
A regular polygon is special type of polygon. Area of Regular Polygon Formula A polygon having equal sides ie. Write down the formula for finding the area of a regular polygon.
To find the area of a regular polygon all you have to do is follow this simple formula. Therefore the area of a regular polygon is given by. To find the area of a regular polygon you use an apothem a segment that joins the polygons center to the midpoint of any side and that is perpendicular to that side segment HM in the following figure is an apothem.
Area of a Regular Polygon Formula However where does this formula come from. A regular polygon is equilateral it has equal sides and equiangular it has equal angles. A regular polygon.
The area of any regular polygon is given by the formula. Apothem is the line from the center of the pentagon to a side intersecting the side at 90 degrees right angle.
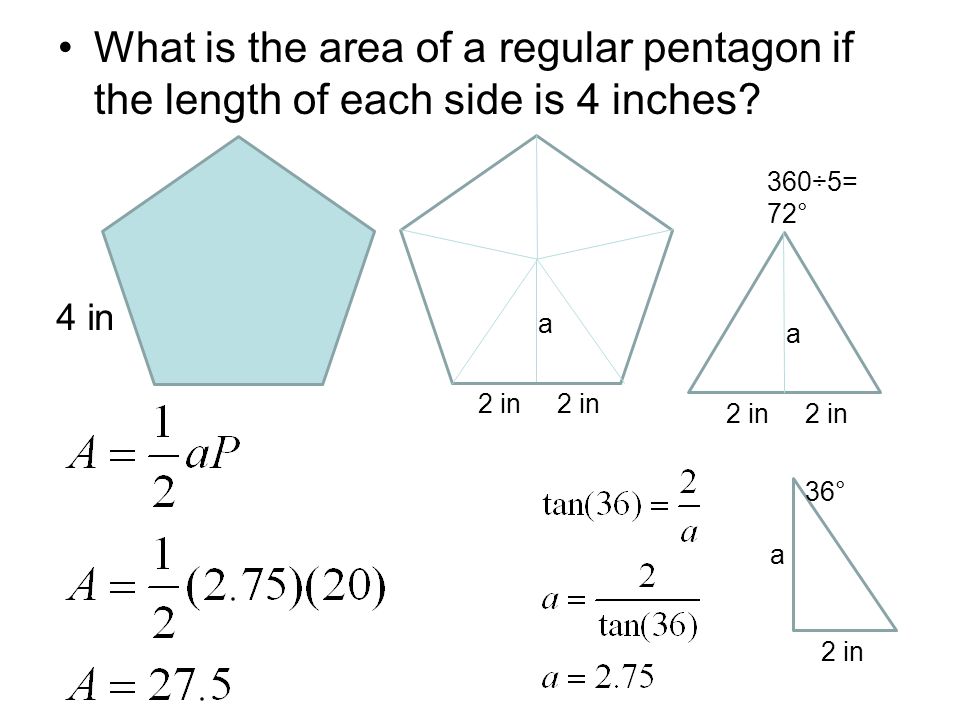
Area of regular pentagon can be found out in 2 ways.
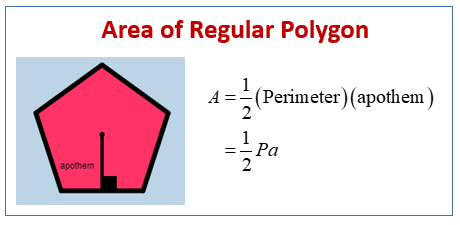
Area of regular pentagon. Area Formula for a Pentagon s is the side of the Pentagon a is the apothem length. Follow these steps to calculate area of pentagon. In a regular pentagon the five sides are equal in length and the internal angles are equal 108 0.
A regular pentagon has. You can still find the area of a regular pentagon if you know. To get the area of the whole polygon just add up the areas of all the little triangles n of them.
A regular polygon is equilateral it has equal sides and equiangular it has equal angles. Write down the pentagon area formula. So all we actually needed to work out the area of 1 of the 5 triangles was the length of the blue line and the length of a sideedge of the Pentagon.
Area of pentagon can be calculated by using the above formula for pentagon area. A little trigonometry The length of one side Each interior angle measures 108 108. Area of a Pentagon A polygon with five sides is called a pentagon.
If you dont know the perimeter calculate it from the side length. Area of one triangle base height 2 side apothem 2. AREA OF PENTAGON 22cm 2 5 110cm 2 What we really needed to know.
P 5s where s is the side length. Polygons can be regular or irregular. And since the perimeter is all the sides n side we get.
Know the correct formula. In Euclidean geometry a regular polygon is a polygon that is equiangular all angles are equal in measure and equilateral all sides have the same length. If the angles are all equal and all the sides are equal length it is a regular polygon.
Where s is the side of the Pentagon and a is the apothem length. Area of pentagon is 52 x s x a. Learn how to find the area of a regular polygon when only given the radius of the the polygon.
Area of Pentagon is given by 52 x s x a. As the polygon is a pentagon having five sides where each side s measures 12 cm its perimeter p is 5 x s 5 x 12 60 cm Now as we know Area A ½ x p x a here p 60 cm and a 75 cm. The area of a cyclic pentagon whether regular or not can be expressed as one fourth the square root of one of the roots of a septic equation whose coefficients are functions of the sides of the pentagon.
Calculate the area of a regular pentagon with side 12 cm and apothem of 75 cm. Area a x p2 where a is the length of the apothem and p is the perimeter of the polygon. The area of a regular polygon is given by the formula below.
Area of a regular pentagon pa 2 where p the perimeter and a the apothem. We go through an example involving a regular pentagon inscrib. Area ½ apothem perimeter Several other area formulas are also available.
Area of Polygon n side apothem 2. 4 Plug the values of a and p in the formula and get the area. Shape with at least three sides.
It can be a simple polygon or a self-intersecting one. Interior Angles of 108 Exterior Angles of 72 Area of approximately 17204774 s2 where sside length. Lets take the pentagon with side length is 5 units and apothem length is 2 units.
Identify and write down the side measurement of the pentagon. Now for the area of the whole Pentagon as there are 5 larger triangles we just multiply 22cm 2 by 5. The regular pentagon is an example of a cyclic pentagon.
Area of Polygon perimeter apothem 2. To find the area of a regular polygon you use an apothem a segment that joins the polygons center to the midpoint of any side and that is perpendicular to that side segment HM in the following figure is an apothem. Regular polygons may be either convex or starIn the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon effectively a straight line.
ads
quizzes for kids age 5
Quiz for 5 year olds Quizzy Kid . Quizzes by age. Quiz for 5 year olds. Quiz for 5 year olds Quiz for 5...
