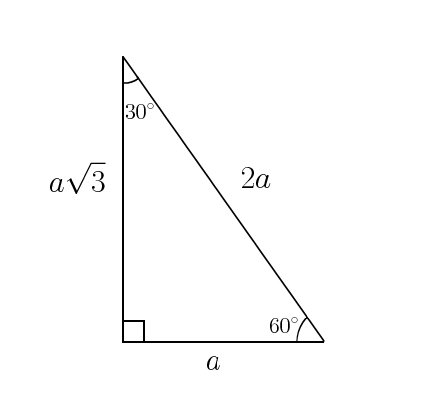
Once we identify a triangle to be a 30 60 90 triangle the values of all angles and sides can be quickly identified. Looking at the diagram we can see that we have a right-angled triangle in which the other two angles are 30 degrees and 60 degrees.

In A 30 60 90 Triangle Where The Shortest Leg Equals 3 What Could The Other Sides Equal Socratic

Find the length of the side x.

Side lengths of a 30-60-90 triangle. A special right triangle is a right triangle having angles of 30 60 90 or 45 45 90. Find the values of 𝑎 and 𝑏. The key characteristic of a 30-60-90 right triangle is that its angles have measures of 30 degrees π6 rads 60 degrees π3 rads and 90 degrees π2 rads.

The following diagram shows a 30-60-90 triangle and the ratio of the sides. The 30-60-90 degree triangle is in the shape of half an equilateral triangle cut straight down the middle along its altitude. The 45-45-90 triangle also referred to as an isosceles right triangle since it has two sides of equal lengths is a right triangle in which the sides corresponding to the angles 45-45-90 follow a ratio of 11 2.

If the longer leg length b is the one parameter given then. It is special because its side lengths are always in the ratio of 1. Each half has now become a 30 60 90 triangle.

It is right triangle whose angles are 30 60 and 90. A 30-60-90 triangle is a particular right triangle because it has length values consistent and in primary ratio. To understand the 30-60 ideal triangle we need to assess a previous topic the equilateral or equiangular triangular.

This doesnt need to be precise however the closer the far better. If we know the shorter leg length a we can find out that. A 30-60-90 right triangle literally pronounced thirty sixty ninety is a special type of right triangle where the three angles measure 30 degrees 60 degrees and 90 degrees.

A 30-60-90 triangle is a special triangle whose angles are 30º 60º and 90º. Because its angles and side ratios are consistent test makers love to incorporate this triangle into problems especially on the no-calculator portion of the SAT. A 30-60-90 triangle is a special right triangle that contains internal angles of 30 60 and 90 degrees.

Lets start by attracting a triangle with all three sides the same length. Imagine cutting an equilateral triangle vertically right down the middle. The side lengths and angle measurements of a 30-60-90 right triangle.

30 60 90 triangle sides. Like the 30-60-90 triangle knowing one side length allows you to determine the lengths of the other sides. Or simply type your given values and the 30 60 90 triangle calculator will do the rest.

The side lengths of a 306090 triangle This is a triangle whose three angles are in the ratio 1. We can see therefore that the side lengths for a 30-60-90 triangle will always have consistent side lengths of x x3 and 2x or x2 3x2 and x. The shortest leg is across from the 30-degree angle the length of the hypotenuse is always double the.

For hypotenuse c known the legs formulas look as follows. Since the triangle is equilateral it is also equiangular and therefore the the angle at B is 60 The height of a triangle is the straight line drawn from the vertex at right angles to the base. 3 and respectively measure 30 π 6 60 π 3 and 90 π 2.

Scroll down the page for more examples and solutions on how to use the 30-60-90 triangle. Luckily for us we can prove 30-60-90 triangle rules true without all ofthis. The leg opposite the 60 angle is of the length of the hypotenuse.

In any 30-60-90 triangle the shortest leg is still across the 30-degree angle the longer leg is the length of the short leg multiplied to the square root of 3 and the hypotenuses size is always double the length of the shorter leg. The sides are in the ratio 1. The ratio of the side lengths of a 30-60-90 triangle are.

Knowledge of the ratio o. In any 30-60-90 triangle you see the following. The Side Lengths of 30-60-90 Triangles Mathematics Find the values of 𝑎 and 𝑏.

The hypotenuse is twice the length of the shortest side. The hypotenuse of the triangle that is the longest side. The lengths of the sides of a 30-60-90 triangle are in the ratio of 132.

The 30-60-90 triangle is a special right triangle and knowing it can save you a lot of time on standardized tests like the SAT and ACT. It has angles of 30 60 and 90. Therefore triangle ADB is a 30-60-90 triangle.

When to Use 30-60-90 Triangle Rules. The theory applies to the side lengths of a 30 60 90 triangle. The leg opposite the 30 angle the shortest side is the length of the hypotenuse the side opposite the 90 angle.

Learn about the special right triangles. The sides of a 30-60-90 right triangle lie in the ratio 132. The triangle is significant because the sides exist in an easy-to-remember ratio.

Luckily for us we can prove 30-60-90 triangle rules true without all ofthis. We can see therefore that a 30-60-90 triangle will always have consistent side lengths of x x3 and 2x or x2 3x2 and x. The ratios of the sides can be calculated using two congruent 30-60-90 triangles.