What is the hypotenuse of a triangle. A hypotenuse is the longest side of a right triangleIts the side that is opposite to the right angle 90.

Right Triangle Altitude Of Right Triangle And The Geometric Mean

Altitude on Hypotenuse Theorem 1 In any right triangle the altitude from the right angle is the geometric mean between the two segments of the hypotenuse Because of these similarities we can conclude two Altitude on Hypotenuse Theorems.

Altitude on hypotenuse theorem. Example of leg theorem. Median response time is 34 minutes and may be longer for new subjects. Xy8x8-y Using Pythagoras theorem the square of the hypotenuse of the right-angled.

It states that the geometric mean of the two segments equals the altitude. Do not approximate 6. It creates two smaller right triangles that are both similar to the original right triangle.

Given the segments of the right triangle we apply the geometric mean theorem or altitude rule and we get the altitude h. When the altitude is drawn to the hypotenuse of a right triangle the altitude is the geometric mean of the hypotenuse segments pretty straight forward 2. If two triangles are similar to each other then.

Figure 2 shows the three right triangles created in Figure. The right triangle altitude theorem or geometric mean theorem is a result in elementary geometry that describes a relation between the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. The hypotenuse is the sum of the segments n and m so we obtain that c n m 312 15 cm.

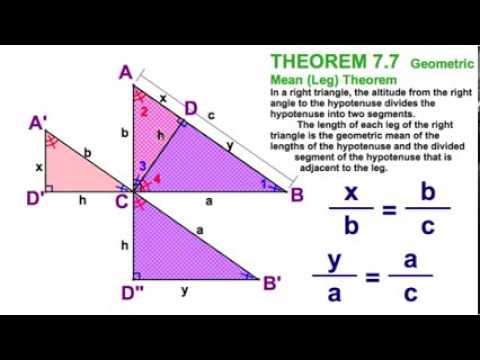
In the figure below find the exact value of y. Geometric Mean Altitude on Hypotenuse Theorem Questions. Leg Theorem Boomerang The length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is adjacent to the leg.

The right triangle altitude theorem or geometric mean theorem is a result in elementary geometry that describes a relation between the lengths of the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. Secondary School Student Grade 7-11 just now Grade 10 Geometry. The altitude drawn to the hypotenuse of a right triangle creates two similar right triangles each similar to the original right triangle and similar to each other.

Right triangleA 30-60-90 triangle is a special right triangle a right triangle being any triangle that contains a 90 degree angle that always has degree angles of 30 degrees 60 degrees and 90 degrees. The altitude of the right triangle is h 6 cm. Hypotenuse length may be found for example from the Pythagorean theorem.

If an altitude is drawn to the hypotenuse of a right triangle as shown in the above figure then note that the two equations in the third part of the theorem are really just one idea not two. Right Triangle Altitude Theorem. In a right triangle the altitude thats perpendicular to the hypotenuse has a special property.

A B C D. When the altitude is drawn to the hypotenuse of a right triangle a leg is the geometric mean of the hypotenuse and the hypotenuse segment adjacent to that leg. It states that the geometric mean of the two segments equals the altitude.

Consider a right angled triangle ABC which is right angled at C. Response times vary by subject and question complexity. Which Triangle is a 30 60 90 Triangle.

Geometric Mean Altitude on Hypotenuse Theorem Questions. Example of altitude theorem. Once weve made these generalizations I have my students document these two important statements 1 and 4 in their notes.

Altitude-on-hypotenuse Theorem In a right triangle the altitude thats perpendicular to the hypotenuse has a special property. Tips to help us recall how to use the theorems. They have been drawn in such a way that corresponding parts are easily recognized.

According to right triangle altitude theorem the altitude on the hypotenuse is equal to the geometric mean of line segments formed by altitude on hypotenuse. This theorem describes the relationship between altitude drawn on the hypotenuse from vertex of the right angle and the segments into which hypotenuse is divided by altitude. If an altitude is drawn to the hypotenuse of a right triangle as shown in the above figure then.

It creates two smaller right triangles that are both similar to the original right triangle.