If every internal angle of a simple polygon is less than 180 the polygon is called convex. The formula for calculating the size of an exterior angle is.
 Find The Measure Of Each Exterior Angle Of The Given Regular Polygon Level 1 Youtube
Find The Measure Of Each Exterior Angle Of The Given Regular Polygon Level 1 Youtube
Exterior angle of regular polygon is given by frac 360 0 n where n is number of sides of a regular polygon.

What is the exterior angle of a regular polygon. The sum of the exterior angles of a regular polygon irrespective of the number of sides is 360 degrees. A Polygon is any flat shape with straight sides. The Exterior Angles of a Polygon add up to 360.
Interior Angles of a Regular Polygon. As you can see for regular polygons all the exterior angles are the same and like all polygons they add to 360 see note below. Regular polygons may be either convex or starIn the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon effectively a straight line.
All the Exterior Angles of a polygon add up to 360 so. The sum of the measures of the interior angles of a polygon with n sides is n 2180. Exterior Angles of a Regular Polygon Exterior angles of every simple polygon add up to 360 360 because a trip around the polygon completes a rotation or return to your starting place.
Where sides meet they form vertices so our hexagon also has six vertices. Each exterior angle must be 360n where n is the number of sides Press play button to see. In Euclidean geometry a regular polygon is a polygon that is equiangular all angles are equal in measure and equilateral all sides have the same length.
The sum of the exterior angles of a polygon is 360. By using this formula easily we can find the exterior angle of regular polygon. For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45.
As a demonstration of this drag any vertex towards the center of the polygon. So each exterior angle is 360 divided by the n the number of sides. The sum of the measures of the exterior angles of a polygon one at each vertex is 360.
Exterior angle of a polygon 360 number of sides. In contrast an exterior angle also called an external angle or turning angle is an angle formed by one side of a simple polygon and a line extended from an adjacent side. They are Supplementary Angles.
An exterior angle is an angle formed between any side and the line extended to its adjacent side. For any given regular polygon to find the each exterior angle we have a formula. On a side note we can use this piece of information in the exterior angle of a polygon formula to solve various questions.
You will see that the angles combine to a full 360 circle. Measure of exterior angle of regular polygon is calculated by dividing the sum of the exterior angles by the number of sides and is represented as MOE360n or Measure of exterior angle 360Number of sides. Since it is a regular polygon the number of sides can be calculated by the sum of all exterior angles which is 360 degrees divided by the measure of each exterior angle.
In the present case there 5 sides in a regular pentagon hence each exterior 3605 or 72 degrees. When the polygons are formed and one of its sides is extended longer than the vertex of a corner the exterior angle of the polygon is formed. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has.
A polygon has exactly one internal angle per vertex. An exterior angle of a polygon is an angle outside the polygon formed by one of its sides and the extension of an adjacent side. There are as many exterior angles as there are sides n and they are all equal.
If N is the number of sides each exterior angle will be 360N degrees. The sum is divided by n to find each exterior angle. The result of the sum of the exterior angles of a polygon is 360 degrees.
Find the regular polygon where each of the exterior angle is equivalent to 60 degrees. In regular polygons the sum of the exterior angles equals 360º ie it forms a circle outside. Formula for exterior angle of regular polygon as follows.
When we add up the Interior Angle and Exterior Angle we get a straight line 180. The exterior angle at a vertex can be obtained by the following formula. The sum of the exterior angles of a regular polygon will always equal 360 degrees.
The sum of exterior angles of a polygon is 360. Measure of a Single Exterior Angle Formula to find 1 angle of a regular convex polygon of n sides 1 2 3 360. Exterior Angles of Polygons The Exterior Angle is the angle between any side of a shape and a line extended from the next side.
Exterior Angle 360 n Exterior Angle 360 n. The number of Sides is used to classify the polygons.
Properties of Interior and Exterior Angles of Polygons. The sum of the measures of the interior angles of a polygon is always 180n-2 degrees where n represents the number of sides of the polygon.
 Sum Of Interior And Exterior Angles In Polygons
Sum Of Interior And Exterior Angles In Polygons
Students also learn the following formulas related to convex polygons.

Sum of interior and exterior angles of a polygon. Therefore the sum of the interior angles of the polygon is given by the formula. The sum of the exterior angles of a regular polygon will always equal 360 degrees. Sum of interior angles p - 2 180.
Sum of all the interior angles of a polygon is equal to the product of a straight angle and two less than the number of sides of the polygon. The sum of its angles will be 180 3 540 The sum of interior angles in a pentagon is 540. The measure of each interior angle of an equiangular n -gon is If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360.
Let n n equal the number of sides of whatever regular polygon you are studying. This method needs some knowledge of difference equation. A pentagon has five sides thus the interior angles add up to 540 and so on.
That is Interior angle Exterior Angle 180 Then we have. Hence we can say if a polygon is convex then the sum of the degree measures of the exterior angles one. Sum of the Interior Angles of a Polygon 180 n-2 degrees Interior Angles of a Polygon Formula.
Exterior Angles Sum of Polygons. It is a bit difficult but I think you are smart enough to master it. The sum of the measures of the exterior angles of a polygon is always 360 degrees.
Sum of interior angles sum of exterior angles n x 180 Sum of interior angles 360 n x 180 Sum of interior angles n x 180 - 360 n-2 x 180 Method 6. This packet includes note sheets and practice problems to teach you about polyons regular polygons convex and concave polygons interior angles and exterior angles. The formula for the sum of that polygons interior angles is refreshingly simple.
The sum of the interior angles of a triangle is 180. An exterior angle of a polygon is made by extending only one of its sides in the outward direction. Its interior angles add up to 3 180 540 And when it is regular all angles the same then each angle is 540 5 108 Exercise.
The sum of the measures of the exterior angles of a convex polygon one at each vertex is 360. In any polygon the sum of an interior angle and its corresponding exterior angle is 180. The sum of interior angles in a quadrilateral is 360º A pentagon five-sided polygon can be divided into three triangles.
This packet will go over what polygons are and how to find their interior and exterior angles. By proving that the sum of the interior angles of a triangle is 180 you will understand that adding two interior angles makes an exterior angle. X Exterior Angle 180 110 Exterior angle 180 Exterior angle 70 So the measure of each exterior angle corresponding to x in the above polygon is 70.
The sum of the measures of the interior angles of a polygon with n sides is n 2180. Sum of Interior Angles Formula. The angle next to an interior angle formed by extending the side of the polygon is the exterior angle.
However not many people understand why it is 180 so lets check beforehand. The sum of the measures of the interior angles of a convex n-gon is n - 2 180 The measure of each interior angle of a regular n-gon is 1n n - 2 180. The sum of the measures of the exterior angles of a polygon one at each vertex is 360.
Interior and exterior angle formulas. There are n sides in the polygon and therefore n straight angles. Each exterior angle of a regular polygon is 360 n where n is the number of sides in the polygon Polygon Exterior Angles Theorem.
They will also make connections to an alternative way to determine the interior angle sum noticing that n -2180 n 180-360. Sum of interior angles n 2 180 S u m o f i n t e r i o r a n g l e s n - 2 180. Measure of a Single Exterior Angle Formula to find 1 angle of a regular convex polygon of n sides 1 2 3 360.
For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has. Here is the formula.
In a regular polygon all the interior angles measure the same and hence can be obtained by dividing the sum of the interior angles by the number of sides. Make sure each triangle here adds up to 180 and check that the pentagons interior angles add up to 540 The Interior Angles of a Pentagon add up to 540. Students will see that they can use diagonals to divide an n -sided polygon into n -2 triangles and use the triangle sum theorem to justify why the interior angle sum is n-2 180.
Exterior angle 180-144 Therefore the exterior angle is 36 The formula to find the number of sides of a regular polygon is as follows. The sum of the measures of all the exterior angles of a polygon is 360.
 Interior And Exterior Angles Of Polygons Youtube
Interior And Exterior Angles Of Polygons Youtube
By using this formula easily we can find the exterior angle of regular polygon.
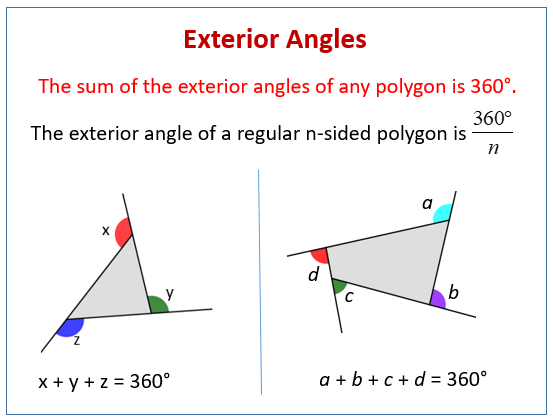
Exterior angle of a polygon formula. Formula for the sum of exterior angles The sum of exterior angles of any polygon is 360. Interior and exterior angle formulas. Together the adjacent interior and exterior angles will add to 180 180.
How to calculate Measure of exterior angle of regular polygon. The formula for calculating the size of an exterior angle is. The Corbettmaths Practice Questions on Angles in Polygons.
The sum of the exterior angles of a polygon is 360. Measure of exterior angle of regular polygon is calculated by dividing the sum of the exterior angles by the number of sides and is represented as MOE360n or Measure of exterior angle 360Number of sides. For our equilateral triangle the exterior angle of any vertex is 120 120.
For a square the exterior angle is 90 90. The sum of the measures of the interior angles of a polygon with n sides is n 2180. Sum of Interior angles of Polygon IA n-2 x 180.
Videos worksheets 5-a-day and much more. Formula for exterior angle of regular polygon as follows. For any given regular polygon to find the each exterior angle we have a formula.
The exterior angle of a regular n-sided polygon is 360n Worksheet using the formula for the sum of exterior angles. 3 6 0 0 n. 180 Regular and Irregular Polygons.
360 div number of sides. Correct answer to the question. Number of Sides of a Regular Polygon 360 Magnitude of each exterior angle.
In any polygon the sum of an interior angle and its corresponding exterior angle is. We can get the equation of interior angles from this. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has.
The sum of the exterior angles of a regular polygon will always equal 360 degrees. In contrast an exterior angle also called an external angle or turning angle is an angle formed by one side of a simple polygon and a line extended from an adjacent side. Exterior Angle Sum Property of Polygon - formula Exterior angle of polygon n 3 6 0 o.
The sum of the measures of the exterior angles of a polygon one at each vertex is 360. The formula to working out the exterior angle of a polygon is this. A polygon has exactly one internal angle per vertex.
Since each exterior angle is equal that means each exterior angle is 360 6 60 degrees. 360 n. Frac 360 0 n n3600.
The number of Sides is used to classify the polygons. 360 Measure of each exterior angle. Formula to find the measure of each exterior angle of a regular polygon when the number of sides n given.
Measure of a Single Exterior Angle Formula to find 1 angle of a regular convex polygon of n sides 1 2 3 360. Interior angle 180 - 360N. 360 divided number of sides So lets use this formula to work out the answer.
For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45. Since you are extending a side of the polygon that exterior angle must necessarily be supplementary to the polygons interior angle. The measure of each interior angle of an equiangular n -gon is If you count one exterior angle at each vertex the sum of the measures of the exterior angles of a polygon is always 360.
Exterior angle of regular polygon is given by. The sum of exterior angles of a polygon is 360. If every internal angle of a simple polygon is less than 180 the polygon is called convex.
In general a regular polygon has exterior angles of 360 N degrees if it has N sides. The formula for calculating the size of an exterior angle in a regular polygon is. Exterior angle of a polygon 360 number of sides.
Interior angle corresponding exterior angle 1800 The sum of the measures of the interior angles of a polygon with n sides is given by the general formula n2180.
We can then rotate that side through an angle of B to reach the next side. S n 2 180 This is the angle sum of interior angles of a polygon.
Conjectures In Geometry Exterior Angles
In any polygon the sum of exterior angles is.
Exterior angle of polygon formula. In a 20-sided polygon one vertex does not send any diagonals. Exterior angle of a polygon 360 number of sides. The exterior angle of the regular polygon with 24 sides is given as the frac 360 0 24 15 0.
How to solve the exterior angles of a polygon. According to the formula number of diagonals n n-3 2. The sum of the internal angle and the external angle on the same vertex is 180.
Sum of Interior angles of Polygon IA n-2 x 180 The measure of an exterior angle of a regular n - sided polygon is given by the formula 360n Exterior angle of a regular polygon EA 360n. The measure of each exterior angle is 72. For example an eight-sided regular polygon an octagon has exterior angles that are 45 degrees each because 3608 45.
Exterior Angles Sum of Polygons. The sum of the exterior angles of a regular polygon will always equal 360 degrees. An exterior angle of a polygon is made by extending only one of its sides in the outward direction.
The sum of the measures of the interior angles of a polygon with n sides is given by the general formula n2180. For an n-gon the sum of the measures of the exterior angles is sum 360. So 11-sided polygon will contain 1111-32 44 diagonals.
The sum of exterior angles of a polygon is 360. The sum of all the internal angles of a simple polygon is 180n2 where n is the number of sidesThe formula can be proved using mathematical induction and starting with a triangle for which the angle sum is 180 then replacing one side with two sides connected at a vertex and so on. The sum of the measures of the exterior angles of a polygon one at each vertex is 360.
Measure of a Single Exterior Angle Formula to find 1 angle of a regular convex polygon of n sides 1 2 3 360. Measure of exterior angle of regular polygon is calculated by dividing the sum of the exterior angles by the number of sides and is represented as MOE360n or Measure of exterior angle 360Number of sides. Hence we can say now if a convex polygon has n sides then the sum of its interior angle is given by the following formula.
360 5. The sum of the measures of the interior angles of a polygon with n sides is n 2180. Formula 3 examples and their solutions.
Notice that corresponding interior and exterior angles are supplementary add to 180. To find the value of a given exterior angle of a regular polygon simply divide 360 by the number of sides or angles that the polygon has. The exterior angle of the regular polygon with 16 sides is given as the frac 360 0 16 225 0.
Find out how many diagonals does that 20-sided polygon contain. The measure of each exterior angle of a regular pentagon is 2x 4. Interior and exterior angle formulas.
The formula for calculating the size of an exterior angle is. Yes we can say what type of polygon. The formula for calculating the size of an exterior angle of a regular polygon is.
Formula 3 examples and their solutions. Formula to find the measure of each exterior angle of a regular n-sided polygon is. For an n-gon the sum of the measures of the exterior angles is sum 360.
If we know exterior angle then can we say what type of polygon is it. Starting at the top side red we can rotate clockwise through an angle of A to reach the angle of the adjacent side to the right. Each exterior angle must be 360n where n is the number of sides Press play button to see.
FAQs on Exterior angle of regular polygon. Lets take a regular hexagon for example. The number of Sides is used to classify the polygons.
So total diagonals contained within an 11-sided polygon 55 -11 ie. Exterior Angle Sum Property of Polygon - formula Exterior angle of polygon n 3 6 0 o. An exterior angle of a polygon is an angle outside the polygon formed by one of its sides and the extension of an adjacent side.
All the Exterior Angles of a polygon add up to 360 so. Solution Detail These four angles are the interior angles of the quadrilateral. Exteriorangleofaregularpolygon 360div numberofsides Remember the interior and exterior.
How to solve the exterior angles of a polygon. An exterior angle of a polygon is an angle at a vertex of the polygon outside the polygon formed by one side and the extension of an adjacent side.